Triclinic (non-orthogonal) simulation boxes

本章定位到HOWTO triclinci (opens new window)

阅读本章你需要：

材料学基础

通常来说，我们模拟时的粒子由正交的模拟盒子包裹。boundary命令设置了边界条件。正交盒子的大小由六个参数来控制，分别是原点(xlo ylo zlo)、顶点(xhi yhi zhi)和边长(lx ly lz)

LAMMPS同样支持三斜体系。三斜盒子同样有它的原点(xlo ylo zlo)，然后定义了三个边向量

$a=(xhi-xlo,0,0)$

$b=(xy,yhi-ylo)$

$c=(xz, yz, zhi-zlo)$

xy xz yz称为倾斜系数(tilt factors)，它们是应用于原本正交长方体的面以将其转换为平行六面体的位移量。

LAMMPS中，$a b c$三个向量不能随意设置。a必须在x正轴上，b在 xy平面指向y轴正方向上，c指向z轴正方向。这也就是要求整个三斜盒子都在第一卦限中，确保是“右手系”。

这些限制不会造成一般性损失，因为可以旋转/反转任何3个晶体基向量集，以便它们符合限制。例如，假设有三个平行六面体的边向量向量 ABC，除了限制他们是个右手系之外没有任何其他限制。通过以下的线性变换，可以将LAMMPS的abc转化为ABC：

$(\mathbf{a} \quad \mathbf{b} \quad \mathbf{c})=\left(\begin{array}{ccc} a_{x} & b_{x} & c_{x} \\ 0 & b_{y} & c_{y} \\ 0 & 0 & c_{z} \end{array}\right)$

$a_{x}=A$

$b_{x}=\mathbf{B} \cdot \hat{\mathbf{A}} \quad=\quad B \cos \gamma$

$b_{y}=|\hat{\mathbf{A}} \times \mathbf{B}|=B \sin \gamma=\sqrt{B^{2}-b_{x}^{2}}$

$c_{x}=\mathbf{C} \cdot \hat{\mathbf{A}} \quad=\quad C \cos \beta$

c_{y}=\mathbf{C} \cdot(\widehat{\mathbf{A} \times \mathbf{B}}) \times \hat{\mathbf{A}} \quad=\frac{\mathbf{B} \cdot \mathbf{C}-b_{x} c_{x}}{b_{y}} c_{z}=|\mathbf{C} \cdot(\widehat{\mathbf{A} \times \mathbf{B}})|=\sqrt{C^{2}-c_{x}^{2}-c_{y}^{2}}

where A = | A | indicates the scalar length of A. The hat symbol (^) indicates the corresponding unit vector. and are angles between the vectors described below. Note that by construction, a, b, and c have strictly positive x, y, and z components, respectively. If it should happen that A, B, and C form a left-handed basis, then the above equations are not valid for c. In this case, it is necessary to first apply an inversion. This can be achieved by interchanging two basis vectors or by changing the sign of one of them.

For consistency, the same rotation/inversion applied to the basis vectors must also be applied to atom positions, velocities, and any other vector quantities. This can be conveniently achieved by first converting to fractional coordinates in the old basis and then converting to distance coordinates in the new basis. The transformation is given by the following equation:

\begin{aligned} &c_{y}=\mathbf{C} \cdot(\widehat{\mathbf{A} \times \mathbf{B}}) \times \hat{\mathbf{A}}=\frac{\mathbf{B} \cdot \mathbf{C}-b_{x} c_{x}}{b_{y}} \\ &c_{z}=|\mathbf{C} \cdot(\widehat{\mathbf{A} \times \mathbf{B}})|=\sqrt{C^{2}-c_{x}^{2}-c_{y}^{2}} \end{aligned}

where V is the volume of the box, X is the original vector quantity and x is the vector in the LAMMPS basis.

可以不要求三斜盒子在任何一个维度上使用周期性边界条件，通常来说还是会在两个维度或以上使用周期性边界条件。

有三种方式来定义三斜体系的9个变量：

• create_box
• read_data
• change_box

正如你所想的，如果将倾斜因子设为0，那就是一个正交盒子，只不过有着三斜盒子的属性。这样你就可以在正交体系下进行弛豫，然后直接用fix deform进行剪切。如果一开始是正交体系，那么就应该用change box进行转换。

为了避免盒子斜得厉害，被压得太平，影响计算效率，LAMMPS通常要求倾斜因子不能超过盒子边长得一半。例如，xlo=2 xhi=12那么x边长就是10，因此xy因子就必须在-5到5之间。同样的，xz和yz都必须在-(xhi-xlo)/2到+(yhi-ylo)/2的范围内。注意这不是一个上下限，因为如果就像刚刚例子中倾斜因子最大是5得话，那么，将其他得设定为-15, -5, 5, 15, 25在几何上就是等效的。在运行过程中，如果超出了这个限度（比如fix deform命令），那么盒子会“啪一下”翻转为一个倾斜因子在上述区间内的等效形状，以便继续运行。细节在fix_deform (opens new window)。反转可以通过flip no取消。这个限制会一直存在，不论是盒子创立得时候，还是使用命令变形得时候。

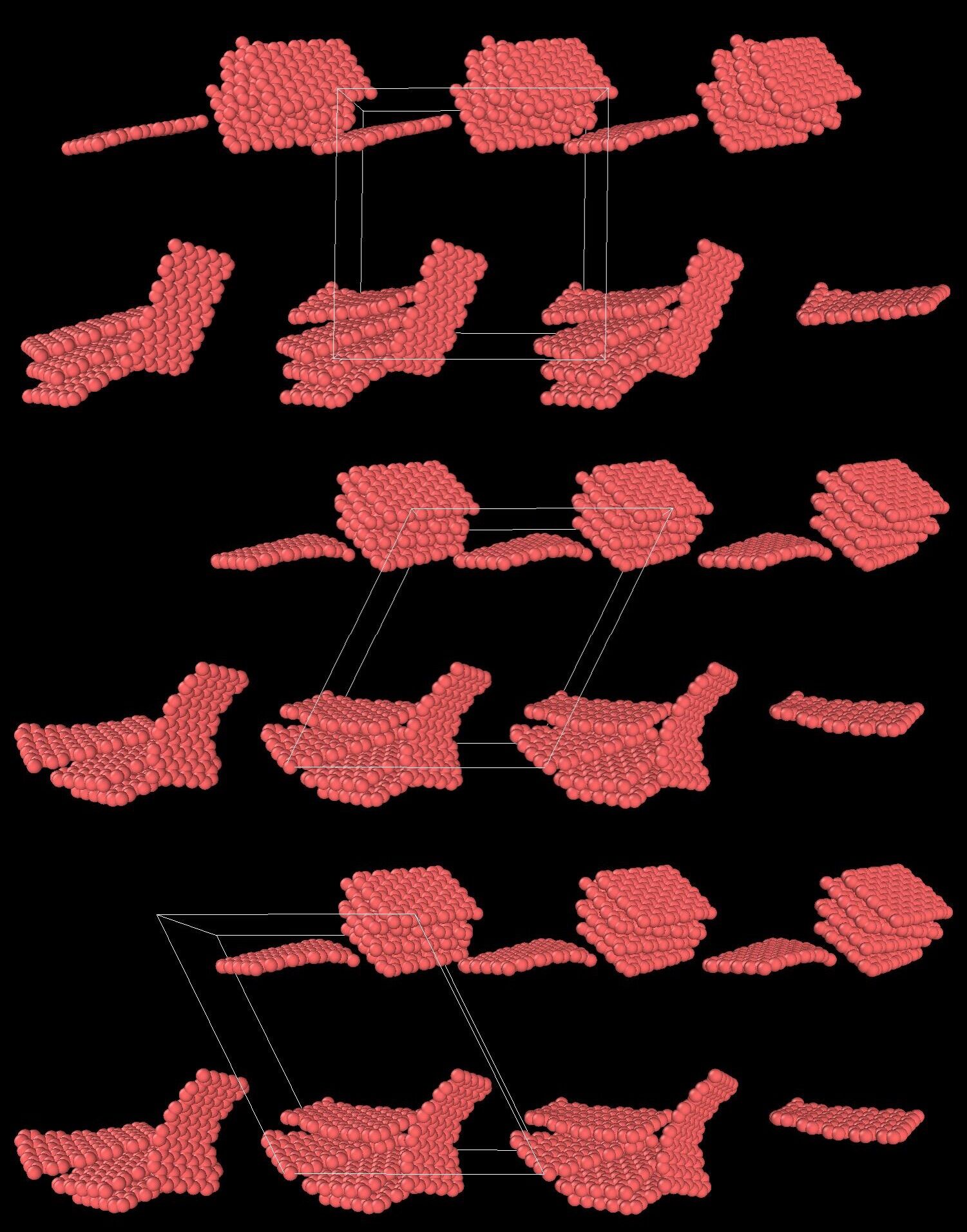
唯一的例外是，如果倾斜因子（x代表xy）中的第一个维度是非周期性的。在这种情况下，对倾斜因子的限制就不强制执行了，因为在该维度上翻转长方体不会由于非周期性而改变原子的位置。在这种模式下，如果将系统倾斜到极端角度，由于模拟框高度倾斜，模拟将变得效率低下。还可以通过box命令取消。

注意，如果一个模拟盒有一个大的倾斜因子，LAMMPS的运行效率会降低，因为在处理器不规则形状的子域周围获取鬼原子需要大量的通信。对于倾斜的极端值，LAMMPS也可能丢失原子并产生误差。

三斜晶体结构有时也用晶体常数$a b c$和$\alpha \beta \gamma$来定义。注意在这种命名法下，$a b c$是边向量的长度abc。关于这六个变量之间、和LAMMPS盒子尺寸、倾斜因子之间的关系的关系，如下所述：

a=\operatorname{lx} b^{2}=\operatorname{ly}^{2}+\mathrm{xy}^{2}

$c^{2}=\mathrm{lz}^{2}+\mathrm{xz}^{2}+\mathrm{yz}^{2}$

$\cos \alpha=\frac{\mathrm{xy} * \mathrm{xz}+\mathrm{ly} * \mathrm{yz}}{b * c}$

$\cos \beta=\frac{\mathrm{xz}}{c}$

$\cos \gamma=\frac{\mathrm{xy}}{b}$

反之则是：

$\mathrm{lx}=a$

$\mathrm{xy}=b \cos \gamma$

$\mathrm{xz}=c \cos \beta$

$\mathrm{ly}^{2}=b^{2}-\mathrm{xy}^{2}$

$\mathrm{yz}=\frac{b * c \cos \alpha-\mathrm{xy} * \mathrm{xz}}{\mathrm{ly}}$

$\mathrm{lz}^{2}=c^{2}-\mathrm{xz}^{2}-\mathrm{yz}^{2}$

$a b c$和$\alpha \beta \gamma$可以通过内置热力学参数cella cellb cellalpha打印出来。

dump文件的帧头格式：

ITEM: BOX BOUNDS xy xz yz
xlo_bound xhi_bound xy
ylo_bound yhi_bound xz
zlo_bound zhi_bound yz

*_bound是为了可视化处理而给出的变量，由以下算出：

xlo_bound = xlo + MIN(0.0,xy,xz,xy+xz)
xhi_bound = xhi + MAX(0.0,xy,xz,xy+xz)
ylo_bound = ylo + MIN(0.0,yz)
yhi_bound = yhi + MAX(0.0,yz)
zlo_bound = zlo
zhi_bound = zhi

One use of triclinic simulation boxes is to model solid-state crystals with triclinic symmetry. The lattice command can be used with non-orthogonal basis vectors to define a lattice that will tile a triclinic simulation box via the create_atoms command.

A second use is to run Parrinello-Rahman dynamics via the fix npt command, which will adjust the xy, xz, yz tilt factors to compensate for off-diagonal components of the pressure tensor. The analog for an energy minimization is the fix box/relax command.

A third use is to shear a bulk solid to study the response of the material. The fix deform command can be used for this purpose. It allows dynamic control of the xy, xz, yz tilt factors as a simulation runs. This is discussed in the next section on non-equilibrium MD (NEMD) simulations.