LAMMPS 中文站

LAMMPS做冲击

5/7/2021

# LAMMPS做冲击

# 什么是冲击压缩？

当外界巨大的冲击能量施加在材料表面，冲击能量会与维持材料原本运动状态的惯性约束同时作用于材料，材料内部将形成应力极高、作用时间极短的冲击波。

冲击波在材料内部传递的短暂过程中，材料的物质种类、物质状态和材料结构会不可逆地进入到一种在平衡加载时不能遇到过的情况，因此，研究这一非平衡过程中应力波的传播与材料/结构的动态响应是冲击压缩科学的基本内涵。

wave

图1 声波的传播

与声波的传播形式类似，冲击波经过的区域，应力水平会出现 十分显著的压力差，推动冲击能量由近及远地传播。区别是， 声波主要作用于气体，冲击波主要作用于固体.

由于冲击压缩的时空尺度（如纳米量级、皮秒量级）都很小，实验难以观察该过程的细节变化，连续介质模拟也不能模拟这一尺度下的原子/分子特性。而分子动力学模拟具有原子尺度分辨率，可以很好地弥补实验与连续介质模拟在这一方面的局限。

下面将简要介绍用LAMMPS模拟冲击压缩的几种方法。

# 如何用LAMMPS模拟冲击压缩？

冲击的模拟方法可分为反射壁法、活塞法（又称“动量镜法”）和MSST法等，模拟方法各有特点，对模拟体系也有不同的要求与限制。

  • 活塞法

活塞法的基本思想如图2所示，使用fix wall/piston命令将材料左侧表面设置为活塞，并设置冲击速度Up，材料左侧表面粒子将以Up的速度向右推进，进而材料内部将产生以速度Us推进的冲击波。

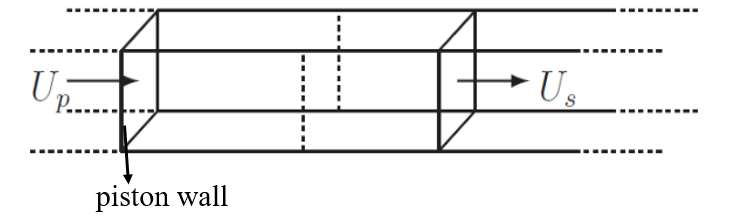piston1 图2 活塞法冲击材料示意图

这一过程的原理如图3所示，将图2中可冲击压缩的连续材料视为一排沿冲击方向连续摆放的材料块，其中最左端块体被视为活塞，活塞以冲击速度Up驱动材料。在这种情况下，活塞以恒定的Up速度运动，并且受到活塞冲击的材料将以与活塞相同的速度运动。可以看出，活塞的运动首先导致前方的材料被“聚集”，即前方材料的密度增加。随后，活塞的推进使材料开始运动，由此产生的密度增加使冲击以速度Us向前运动。

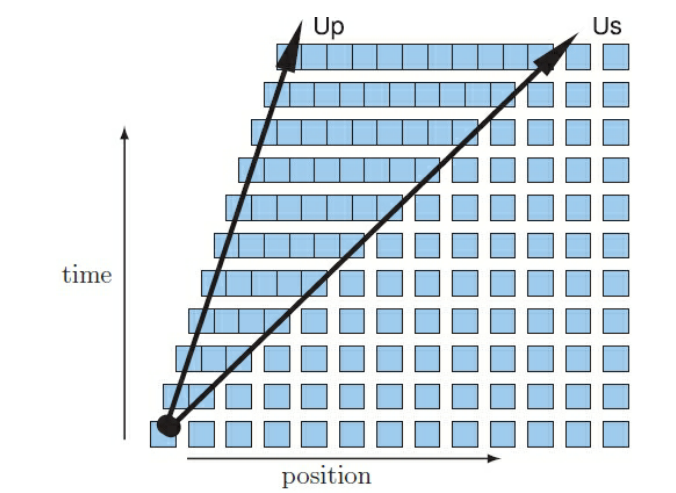piston2 图3 活塞驱动冲击的原理图

命令详解：

fix ID group-ID wall/piston face ... keyword value ...

    face = zlo

    zero or more keyword/value pairs may be appended

    keyword = pos or vel or ramp or units

        pos args = z
            z = z coordinate at which the piston begins (distance units)

        vel args = vz
            vz = final velocity of the piston (velocity units)

        ramp = use a linear velocity ramp from 0 to vz
            ramp args = target damp seed extent
                target = target velocity for region immediately ahead of the piston
                damp = damping parameter (time units)
                seed = random number seed for langevin kicks
                extent = extent of thermostatted region (distance units)

        units value = lattice or box
            lattice = the wall position is defined in lattice units
            box = the wall position is defined in simulation box units
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

此命令将一个壁面设置为质量无限大的运动活塞，该活塞像“动量镜”（Momentum mirror technique）一样，能反射指定组中的粒子，例如，当指定组中的粒子静止不动、活塞以Up速度冲击静止粒子时，静止粒子将被赋予2*Up的运动速度。

face和pos定义了设置的活塞位置，目前face只能是zlo，并沿着z轴正向运动。

vel和ramp定义了活塞的速度。若只使用vel而不使用ramp，活塞将以vel定义的恒定速度运动；若使用ramp，活塞的运动速度将线性变化，且活塞前的区域由langevin恒温器控温，区域随活塞一起运动，区域大小由extent定义。

注意，使用该命令前，需要安装SHOCK软件包；设置活塞的表面必须是s型边界，其相对面可以是除周期性外的任何类型边界；该命令通过直接置换粒子来形成活塞，而不是对它们施加一个力，因此，该方法不适用于含刚体粒子的体系。

  • 反射壁法

反射壁法的基本思想与活塞法的冲击形式恰好相反，在反射壁法中，保持反射壁不动，粒子以速度Up冲击反射壁，材料内部将产生方向与Up方向相反，速度为Us的冲击波，如图4所示。

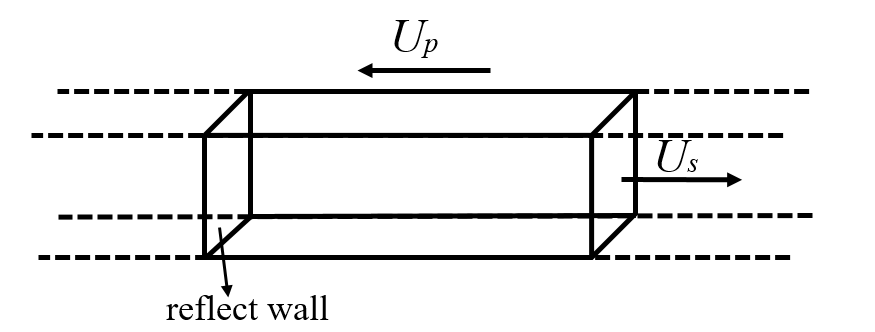reflect 图4 反射壁法冲击材料示意图

命令详解：

fix ID group-ID wall/reflect face arg ... keyword value ...

    face = xlo or xhi or ylo or yhi or zlo or zhi

    arg = EDGE or constant or variable
        EDGE = current lo edge of simulation box
        constant = number like 0.0 or 30.0 (distance units)
        variable = equal-style variable like v_x or v_wiggle

    keyword = units

    units value = lattice or box
        lattice = the wall position is defined in lattice units
        box = the wall position is defined in simulation box units
1
2
3
4
5
6
7
8
9
10
11
12
13
14

此命令将一个或多个壁面设置为反射壁，当指定组中的粒子以速度Up穿过这些壁面时，壁面将赋予这些粒子-Up的速度去反射它们。

face arg指出了设置的反射壁的位置，可以是EDGE、常数或变量。

keyword value指出了arg-constant中距离单位的含义。

注意，反射壁所在的维度必须是非周期性的；该命令通过直接置换粒子来形成反射壁，而不是对它们施加一个力，因此，如果体系中的粒子为刚体，应使用软壁来代替该命令，如fix wall/lj93、fix wall/ harmonic命令。

  • MSST法

直接使用非平衡分子动力学模拟冲击波的传播（如活塞法和反射壁法）需要很大的系统尺寸和计算成本。Reed等人提出了一种多尺度激波技术(multiscale shock technique, MSST)，该方法基于Navier−Stokes方程，结合分子动力学和一维欧拉方程来模拟可压缩流动中激波的传播，以有效地涵盖大的时空尺度。

在MSST方法中，通过改变模拟单元的体积和温度，使整个系统的运动规律遵循冲击Hugoniot关系（该关系符合冲击波的宏观守恒定律），而无需设计很大尺寸的模拟体系，去维系足够长的冲击时间，使体系粒子运动达到冲击Hugoniot标准，因此计算成本被大大降低。

详细案例请参考：lammps\Examples\msst

限制方法