LAMMPS做拉伸与剪切

本章定位到fix_deform (opens new window)

阅读本章你需要：

工程力学基础

使用LAMMPS，不仅可以做平衡热力学，亦可以做非平衡热力学。fix deform命令提供了一种对盒子拉伸与剪切变形、对粒子群进行仿射变换的功能。正交盒子有x y z三个可调整的参数，三斜盒子有x y z xy xz yz六个。任何一个都可以通过fix deform命令进行独立或者同步得调整。fix deform命令的原理是，每经过N步，盒子做一次拉伸或压缩或剪切，然后将粒子的位置、速度和各种向量(per-atom vector)映射到新的位置。在变形的过程中，所有不由deform控制的参数仍由系综控制。

由于算力的限制，我们计算的时间都是在皮秒到纳秒级别，而现实中则是秒级，因此盒子的变形速度与现实中相差极大。所以对于这种非平衡分子动力学（non-equilibrium MD, NEMD），一个最基本的问题是需要将盒子变形的速度从粒子的总速度中减去，只剩下热运动的速度，以保证所有的热力学参数正常。因此fix deform命令需要配合其他的命令使用。

拉伸与压缩

fix ID group-ID deform N direct style value ... keyword value ...

direct := x or y or z 

style value(s):

    style = final or delta or scale or vel or erate or trate or volume or wiggle or variable

    final values = lo hi
        lo hi = box boundaries at end of run (distance units)
      
    delta values = dlo dhi
        dlo dhi = change in box boundaries at end of run (distance units)
    
    scale values = factor
        factor = multiplicative factor for change in box length at end of run
      
    vel value = V
        V = change box length at this velocity (distance/time units),
            effectively an engineering strain rate
      
    erate value = R
        R = engineering strain rate (1/time units)
      
    trate value = R
        R = true strain rate (1/time units)
      
    volume value = none 
        adjust this dim to preserve volume of system
      
    wiggle values = A Tp
        A = amplitude of oscillation (distance units)
        Tp = period of oscillation (time units)
      
    variable values = v_name1 v_name2
        v_name1 = variable with name1 for box length change as function of time
        v_name2 = variable with name2 for change rate as function of time

keyword value(s)：
    remap value = x or v or none
        x = remap coords of atoms in group into deforming box
        v = remap velocities of all atoms when they cross periodic boundaries
        none = no remapping of x or v

    flip value = yes or no
        allow or disallow box flips when it becomes highly skewed

    units value = lattice or box
        lattice = distances are defined in lattice units
        box = distances are defined in simulation box units

x y z指出了变形的方向。

final delta scale vel erate都是使盒子尺寸从初始值到最终值随时间线性变化，因此本质上是“恒定工程应变率”。

final 指定变形方向上的最终边界。lo(low) 和hi(high)的值的单位是当前模拟的长度单位。

delta指定的是变形结束时变形方向上的变化量。

scale指定的是变形方向上的变化倍率。举个栗子，如果盒子初始长度是10，倍率因子是1.1的话，那么最终值将是11；反之，如果小于1，盒子将被压缩。

vel指定了变形的速度，单位时distance/time。举个例子，如果开始时盒子是100埃，变形速度时10埃每皮秒，那么10皮秒后就是200埃长。即长度时间函数为$ L(t)=L_0+V*dt $

erate指定恒定工程应变率，单位1/time。拉伸应变是没有应变的，定义为δL/L0(变化量比原始量)。因此变形方向上的长度时间函数为$ L(t)=L_0(1+erate*\Delta t) $.

trate是恒定的真实应变速率，而不是工程拉伸速率。真实，意为，长度的变化并不是从起始值到终值线性变化的。但是同样，单位是1/time。长度时间函数为$ L(t)=L_0*\exp(trate*\Delta t) $另外，erate和trate都是可以作用在多个方向上的，前提是你得计算好三者的值。

volume是保持整个盒子体积不变。还是用例子说话。当我parameter设置为“x erate 1e-5 y erate 1e-5 z volume”时，意味着我确定了x，y的拉伸速率，而在盒子保持体积不变的情况下，z随之而动。

wiggle给盒子一个简谐的动态拉伸: $L(t)=L_0+A\sin(2*\pi *\frac{t}{T})$

variable其后跟变量表达式。

另：所有的变形都是以盒子中点为基准的。

For solids or liquids, note that when one dimension of the box is expanded via fix deform (i.e. tensile strain), it may be physically undesirable to hold the other 2 box lengths constant (unspecified by fix deform) since that implies a density change. Using the volume style for those 2 dimensions to keep the box volume constant may make more physical sense, but may also not be correct for materials and potentials whose Poisson ratio is not 0.5. An alternative is to use fix npt aniso with zero applied pressure on those 2 dimensions, so that they respond to the tensile strain dynamically.

engineering strain & true strain ?

回顾一下两个应变的区别。

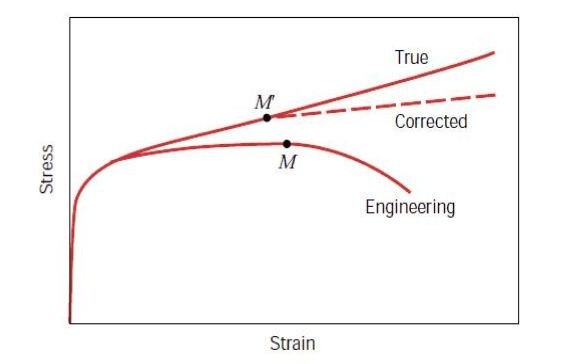
圆柱试样在拉伸时候的应力-应变曲线。我们定义工程应力$\sigma_e =\frac{F_N}{A}$，工程应变$\epsilon_e =\frac{l-l_0}{l_0}$。其中$A$是拉伸前试样的横截面积，$l_0$是拉伸前的长度。

但是，随着拉伸会出现颈缩的现象，这时由于横截面积减小，计算出的工程应力就会相应增大。所以说，工程应力是为了测试的简便而采取的估计。我们定义真实应力$\sigma_t =\frac{F_N}{A_i}$。由体积不变性推导出真实应变$\epsilon_t=\ln(\frac{l_i}{l_0})$。其中$A_i$指的是颈缩区域的真实截面积（cross-sectional area）。真实应力应变与工程应力应变之间的关系是：

$\sigma_t=(1+\epsilon_e)*\sigma_e$

$\epsilon_t = ln(1+\epsilon_e)$

剪切

fix ID group-ID deform N direct style value ... keyword value ...

direct := xy or xz or yz 

style value(s):

    final tilt
        tilt factor at end of run (distance units)
    
    delta dtilt
        dtilt = change in tilt factor at end of run (distance units)

    vel V
        V = change tilt factor at this velocity (distance/time units),
            effectively an engineering shear strain rate
      
    erate R
        R = engineering shear strain rate (1/time units)
      
    trate R
        R = true shear strain rate (1/time units)
      
    wiggle A Tp
        A = amplitude of oscillation (distance units)
        Tp = period of oscillation (time units)
      
    variable v_name1 v_name2
        v_name1 = variable with name1 for tilt change as function of time
        v_name2 = variable with name2 for change rate as function of time

xy xz yz是剪切的方向。变化倾斜因子的时候不会改变三斜盒子的体积。

final, delta, vel, and erate都会以恒定的工程剪切拉伸速率进行，意味着倾斜因子会随时间线性变化。

同拉伸压缩一样，final指定了结束时的倾斜因子的值，delta是变化值，vel实际上是工程剪切应变率（engineering shear strain rate）$rate=V/L_0$，其中$L_0$是剪切方向上起始的盒子长度。For example, if the initial tilt factor is 5 Angstroms, and the V is 10 Angstroms/ps, then after 1 ps, the tilt factor will be 15 Angstroms. After 2 ps, it will be 25 Angstroms.

erate是恒定工程剪切应变率（constant engineering shear strain rate），单位是 1/时间。剪切形变是无量纲的，定义为剪切方向上的位移除以盒子垂直于这个方向的盒子长度。

倾斜因子T是对时间的函数

$T(t) = T0 + L0*e_{rate}*dt$

where T0 is the initial tilt factor, L0 is the original length of the box perpendicular to the shear direction (e.g. y box length for xy deformation), and dt is the elapsed time (in time units). Thus if erate R is specified as 0.1 and time units are picoseconds, this means the shear strain will increase by 0.1 every picosecond. I.e. if the xy shear strain was initially 0.0, then strain after 1 ps = 0.1, strain after 2 ps = 0.2, etc. Thus the tilt factor would be 0.0 at time 0, 0.1ybox at 1 ps, 0.2ybox at 2 ps, etc, where ybox is the original y box length. R = 1 or 2 means the tilt factor will increase by 1 or 2 every picosecond. R = -0.01 means a decrease in shear strain by 0.01 every picosecond.

The trate style changes a tilt factor at a “constant true shear strain rate”. Note that this is not an “engineering shear strain rate”, as the other styles are. Rather, for a “true” rate, the rate of change is constant, which means the tilt factor changes non-linearly with time from its initial to final value. The units of the specified shear strain rate are 1/time. See the units command for the time units associated with different choices of simulation units, e.g. picoseconds for “metal” units). Shear strain is unitless and is defined as offset/length, where length is the box length perpendicular to the shear direction (e.g. y box length for xy deformation) and offset is the displacement distance in the shear direction (e.g. x direction for xy deformation) from the unstrained orientation.

The tilt factor T as a function of time will change as

$T(t) = T0 exp(t_{rate}*dt)$

where T0 is the initial tilt factor and dt is the elapsed time (in time units). Thus if trate R is specified as ln(1.1) and time units are picoseconds, this means the shear strain or tilt factor will increase by 10% every picosecond. I.e. if the xy shear strain was initially 0.1, then strain after 1 ps = 0.11, strain after 2 ps = 0.121, etc. R = ln(2) or ln(3) means the tilt factor will double or triple every picosecond. R = ln(0.99) means the tilt factor will shrink by 1% every picosecond. Note that the change is continuous, so running with R = ln(2) for 10 picoseconds does not change the tilt factor by a factor of 10, but by a factor of 1024 since it doubles every picosecond. Note that the initial tilt factor must be non-zero to use the trate option.

Note that shear strain is defined as the tilt factor divided by the perpendicular box length. The erate and trate styles control the tilt factor, but assume the perpendicular box length remains constant. If this is not the case (e.g. it changes due to another fix deform parameter), then this effect on the shear strain is ignored.

The wiggle style oscillates the specified tilt factor sinusoidally with the specified amplitude and period. I.e. the tilt factor T as a function of time is given by

$T(t) = T_0 + A sin(2*pi t/T_p)$

where T0 is its initial value. If the amplitude A is a positive number the tilt factor initially becomes more positive, then more negative, etc. If A is negative then the tilt factor initially becomes more negative, then more positive, etc. The amplitude can be in lattice or box distance units. See the discussion of the units keyword below.

The variable style changes the specified tilt factor by evaluating a variable, which presumably is a function of time. The variable with name1 must be an equal-style variable and should calculate a change in tilt in units of distance. Note that this distance is in box units, not lattice units; see the discussion of the units keyword below. The formula associated with variable name1 can reference the current timestep. Note that it should return the “change” in tilt factor, not the absolute tilt factor. This means it should evaluate to 0.0 when invoked on the initial timestep of the run following the definition of fix deform.

The variable name2 must also be an equal-style variable and should calculate the rate of tilt change, in units of distance/time, i.e. the time-derivative of the name1 variable. This quantity is used internally by LAMMPS to reset atom velocities when they cross periodic boundaries. It is computed internally for the other styles, but you must provide it when using an arbitrary variable.

Here is an example of using the variable style to perform the same box deformation as the wiggle style formula listed above, where we assume that the current timestep = 0.

variable A equal 5.0
variable Tp equal 10.0
variable displace equal "v_A * sin(2*PI * step*dt/v_Tp)"
variable rate equal "2*PI*v_A/v_Tp * cos(2*PI * step*dt/v_Tp)"
fix 2 all deform 1 xy variable v_displace v_rate remap v

LAMMPS中，倾斜因子通常不能超过边长的一半（三斜盒初步中讲过）。

为了服从这个限制，允许大剪切形变，将采用下面这种算法。如果倾斜因子超过边长的一半，那么盒子将会反转到另一边，所有的原子重映射到合适的位置，然后模拟继续。举个例子来讲，如果xy起始是0，xy final 100.0，lx是10，和上例一致，那么xy从0增加到5.0，到达了一半的临界，紧接着反转到-5.0，在增加到5.0，如此往复十次，直到到达100。

一个例外是，如果倾斜因子中的第一维（xy中的x）不是周期边界条件的。这种情况下，对倾斜因子的限制不是强制的，因为反转盒子之后这一维度上由于非周期边界条件限制不能对原子重映射。在这种模式下，如果将盒子剪切倾斜到极端的角度，不但计算效率极其低下而且会报错。

每当盒子的尺寸形状改变，remap决定原子的位置是不是要重映射到新的盒子中。如果按照默认，重映射参数为x，在fix deformgroup中的原子将被重映射，反之其他不在group-ID范围内的将不会。需要注意的是，仅仅是原子的坐标会变化而速度不会。如果重映射参数选择v，那么在group中所有的原子再穿过边界的时候都会根据两侧的速度差调整本身的速度。

区别在于，x是粗暴地将原子映射到新盒子上，这通常只适合固体。如果想让原子“随着盒子移动”，也就是说盒子扩大，原子以盒子扩大的速率随之扩散，那就选择v。如果什么都不要，就是想让盒子变形然后让原子自然扩散，那就选none。

当进行非平衡分子动力学时，remap v基本上必须要设定。因为fix nvt/sllod调整原子的位置和速度，从而得到与不断变化的盒子大小/形状相匹配的速度分布。因此，原子坐标不应通过fix deform重新映射，而应在原子穿过周期性边界的时候重新映射，这与fix nvt/sllod创建的速度剖面保持一致。如果remap设置与fix nvt/sllod不一致，将抛出一个警告。

当进行流体的非平衡分子动力学时，remap v基本上必须要设定。流体要求流的速度分布要和变形的盒子保持一致。就如上一段提到，fix nvt/sllod或者fix langevin（与compute temp/deform配合使用）等恒温器通常可以做到。如果不使用恒温器，将没有驱动力使粒子的行为与变形的盒子保持一致。例如，剪切是下层速度为零，上层为10，但可能速度梯度从-5到+5。可以通过fix ave/chunk，compute temp/deform和compute temp/profile来监控这种变化。减少这种情况的一种方式是用velociy ramp给一个初始的速度分布，来符合盒子的变形速率。这也可以使系统更快地达到平衡。

对于流体，remap v的时候一定要选择合适的恒温器，例如fix nvt/sllod 或者fix langevin，否则将会缺少原子运动的驱动力。如果盒子是一个剪切变形，各处的变形速率不一致，那么为了更快达到平衡，需要通过velocity ramp来使原子速率于盒子应变率一致。

如果体系中有fix rigid定义的刚体，那么remap x将会将质心映射到合适的位置，无论其他的部分如何分布或者是否在fix deform group中。即便是remap v也不会重映射速度，因为fix nvt/sllod命令不会特殊对待刚体。如果想在刚体上应用非平衡热力学，可以对其单独使用恒温器或者将其置于背景溶液中然后对溶液使用fix nvt/sllod。

flip控制三斜盒子会不会在倾斜因子超过临界值时反转盒子。如果flip yes，将会按照上述的算法反转。flip no倾斜因子继续增大而不会继续反转。在大形变下，由于体积不变，盒子会变得非常长因此计算是极其无效率的，极限下将可能会丢失原子并报错。

unit可重新指定单位。默认使用的是盒子本身的长度单位，例如在real或者metal下的埃。lattice可以使用晶格间距为单位，但是之前必须先用lattice定义。单位的选择也会影响vel参数，因为他是根据距离/时间定义的。同样需要注意的是，units不会影响到variable。如果使用lattice，应在定义variable公式的时候使用xlat ylat zlat这样的关键词。